redis中的三种不常见数据类型之bitmap
除了常见的五种数据类型之外,在redis的高版本中,开始支持一些相对高级的数据结构;下面介绍一下redis中的位图(bitmap)。
bitmap
介绍
bitmap即位图,redis在2.2.0及以上版本开始支持。位图的功能是支持基本的位操作,可以通过给定的api修改或者读取数据中某个位上的值。虽然bitmap新增了相关的api,但本质上在redis中还是以字符串的形式存储的。
比如big这个字符串,在redis中以如下二进制存储;如果通过setbit指令,将第8位置为1,则字符串的值就变成了cig,这和通过set命令将值更新为cig是相同的效果。

setbit和getbit
127.0.0.1:6379> set bitmap big
OK
127.0.0.1:6379> setbit bitmap 7 1 #给位图指定索引设置值
(integer) 0
127.0.0.1:6379> get bitmap
"cig"
127.0.0.1:6379> getbit bitmap 7 #获取位图指定索引的值
(integer) 1
127.0.0.1:6379> getbit bitmap 6
(integer) 1
127.0.0.1:6379>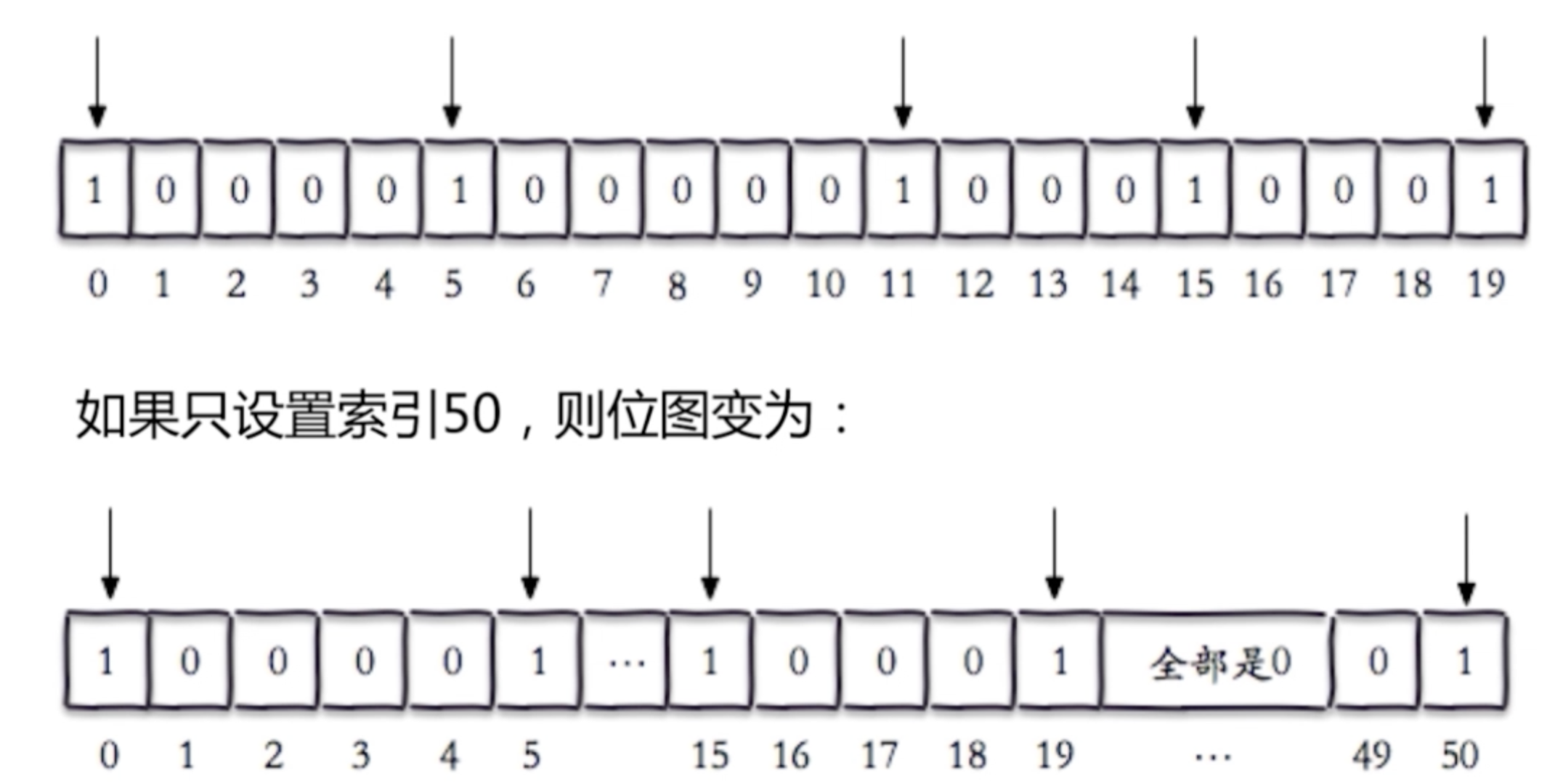
127.0.0.1:6379> setbit bitmap 50 0
(integer) 0
127.0.0.1:6379> get bitmap
"cig\x00\x00\x00\x00"
127.0.0.1:6379> setbit bitmap 50 1
(integer) 0
127.0.0.1:6379> get bitmap
"cig\x00\x00\x00 "如果设置一个很大索引值,那么这个字符串会动态扩容到对应的长度。由于这个特性,offset过大,会导致耗时比较长,有阻塞风险。我们知道在redis中String最大为512M,因此offset也是有最大值的。此外setbit指令不会重置对应Key的过期时间戳。
在一台2010MacBook Pro上,测试结果如下:
| offset值 | 分配内存大小(MB) | 耗时(ms) |
|---|---|---|
| 2^32-1 | 512 | 300 |
| 2^30-1 | 128 | 80 |
| 2^28-1 | 32 | 30 |
| 2^26-1 | 8 | 8 |
除了setbit和getbit这两个指令外,还有bitcount,bitop以及bitpos三个指定。它们的作用分别如下:
bitcount
用于计算bitmap中,指定范围内1的个数,注意这里的start和end值不是offset,它们的单位是字节,比如:bitcount bitmap 0 1是计算第一个字节中有多少位为1。
127.0.0.1:6379> get bitmap
"big"
127.0.0.1:6379> bitcount bitmap 0 1
(integer) 7
127.0.0.1:6379> bitcount bitmap 1 2
(integer) 9
127.0.0.1:6379> type bitmap
string
127.0.0.1:6379>bitop
用于对bitmap集合做操作,例如:and(与),or(并),xor(异或),not(对某个集合取反),操作的结果放到指定的目标key中。
127.0.0.1:6379> set bitmap1 a
OK
127.0.0.1:6379> set bitmap2 b
OK
127.0.0.1:6379> bitop and bitmap3 bitmap1 bitmap2
(integer) 1
127.0.0.1:6379> get bitmap3
"`"
127.0.0.1:6379> bitop or bitmap3 bitmap1 bitmap2
(integer) 1
127.0.0.1:6379> get bitmap3
"c"
127.0.0.1:6379> bitop xor bitmap3 bitmap1 bitmap2
(integer) 1
127.0.0.1:6379> get bitmap3
"\x03"
127.0.0.1:6379> bitop not bitmap3 bitmap1
(integer) 1
127.0.0.1:6379> get bitmap3
"\x9e"
127.0.0.1:6379>bitpos
用于计算bitmap中,第一次出现1或者0的位置(offset)。
127.0.0.1:6379> set bitmap big
OK
127.0.0.1:6379> getbit bitmap 0
(integer) 0
127.0.0.1:6379> getbit bitmap 1
(integer) 1
127.0.0.1:6379> getbit bitmap 2
(integer) 1
127.0.0.1:6379> getbit bitmap 3
(integer) 0
127.0.0.1:6379> bitpos bitmap 1 0 3
(integer) 1
127.0.0.1:6379>应用
计算DAU
位图(bitmap)在某些场景下可以很方便的用来计算日活量(DAU),比如有一个1亿用户,日活量可能到达5千万的系统;如果需要统计某段时间内,活用用户数的话,首先想到的可能是用集合来做,比如每天,都将活跃用户的id存储到一个指定的集合当中,然后计算这个集合的大小就可以得到日活数;也可以用这个集合来判断某个用户是否在该集合中,用来判断某个用户在某天是否上线过。
除了直接采用集合这种方式,也可以使用位图来存储。前提是每个用户都可以用唯一的一个正整数来表示,比如用户Id是个bigInt类型的正整数,这就很适合这种场景。如果用户在某天上线了,只需要将该bit位置为1即可,求上线用户数,就变成了求bitmap中1的个数,求某个用户是否在某天上线,就可以转化为求bitmap中对应位是否为1。
此外在一定情况下,采用bitmap,比直接采用集合更加节省空间。
| 数据类型 | 每个userId占用的空间 | 需要存储的用户量 | 全部内存 |
|---|---|---|---|
| Set | 32(假设是int) | 50,000,000 | 200M |
| Bitmap | 1bit | 100,000,000 | 12.5M |
实现bloomFilter
介绍下布隆过滤器
BloomFilter是一个很有名的数据结构,它是由一个长度为m比特的位数组(bit array)与k个哈希函数(hash function)组成的数据结构。位数组均初始化为0,所有哈希函数都可以分别把输入数据尽量均匀地散列。这种数据结构特别适合用来解决一些存在性问题——即判断某个元素是否在某个集合当中。
一般的集合,比如HashSet之类的,存在一些不足。当集合当中元素的个数特别大的时候,占用的空间会非常大,同时出现哈希碰撞的概率也将增大。而BF(bloomFilter)在一定程度上解决了这个问题。
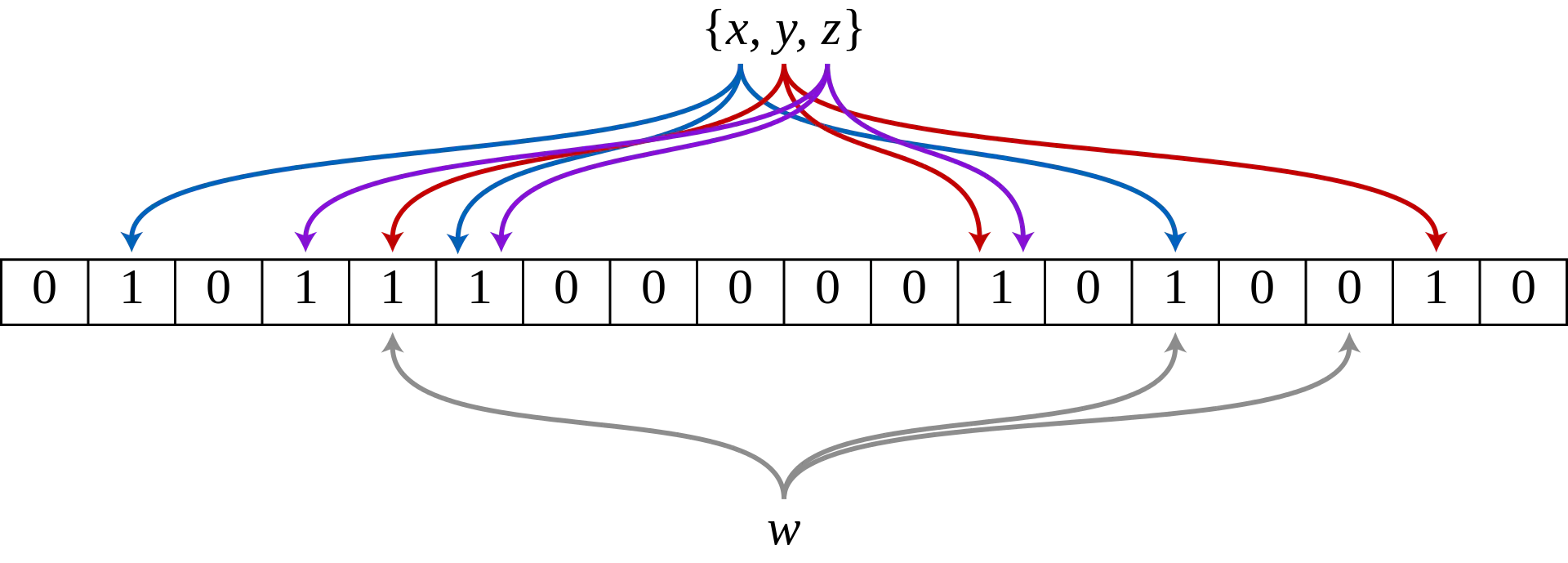
以上图作为一个例子,介绍一下BF的工作流程。首先这个BF由18个bit数组以及3个哈希函数组成。初始化时,所有bit位都是0,在往集合中加入元素时,依次利用每一个哈希函数计算元素的哈希值,然后将哈希值映射到m数组上,并将对应bit位置为1。将全部元素添加完成后,BF就初始化好了。此时,就可以用来判断一个新元素w,是否在这个{x,y,z}集合当中;首先和添加元素时类似,依次用哈希函数计算w的值,然后映射到m数组上,然后看数组上对应的bit位是否都是1,如果都是1,则说明w可能存在该集合当中,如果存在某次哈希值映射位上是0,则说明w一定不存在这个集合当中。
通过上面的表述,可以知道BF有如下特性——如果判断结果是不在集合中,那么该元素一定不在该集合当中;如果判断结果是在集合当中,那么只能说该元素可能在集合当中。
为什么说只是可能在集合当中呢?因为存在哈希冲突的可能,即k个哈希函数计算的值,都存在冲突,这样即使新元素w的哈希值的k个映射位都是1,也不能说明w就一定存在集合当中;而只能说这种可能性比较大。可以用上图来做简单说明,假如w最后一次映射的bit位也是1,那么w就满足所有映射位都是1的条件,但是w这个元素确实是个新元素,即出现了假阳性(False Positive)概率事件。
总结
BF优点:
不需要存储数据本身,只用比特表示,因此空间占用相对于传统方式有巨大的优势,并且能够保密数据;
时间效率也较高,插入和查询的时间复杂度均为O(k);
哈希函数之间相互独立,可以在硬件指令层面并行计算;BF缺点:
只能插入和查询元素,不能删除元素,这与产生假阳性的原因是相同的;
存在假阳性的概率,不适用于任何要求100%准确率的情境;
假阳性概率的计算
那么在实际应用当中,如何来计算假阳性概率呢?这里给一个简单推导过程。
假设拿一个不存在于集合中的新元素,在已经插入n个元素,位数组长度为m,hash函数有k个的BF中进行存在性判断:
- 位数组中某一特定的位在进行元素插入时的 Hash 操作中没有被置位的概率是:1-1/m
- 在所有k次Hash操作后该位都没有被置1的概率是: (1-1/m)^k
- 如果我们插入了 n 个元素,那么某一位仍然为 “0” 的概率是:(1-1/m)^kn
- 该位为1,即被置位的概率是:1-(1-1/m)^kn
- 经过k次Hash操作,每次对应的位置均为1(即假阳性)概率为: (1-(1-1/m)^kn)^k
然后根据极限推导,可以得到如下公式:
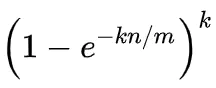
其中:
e:常数
n:插入元素的个数
m:bit数组的长度
k:哈希函数个数
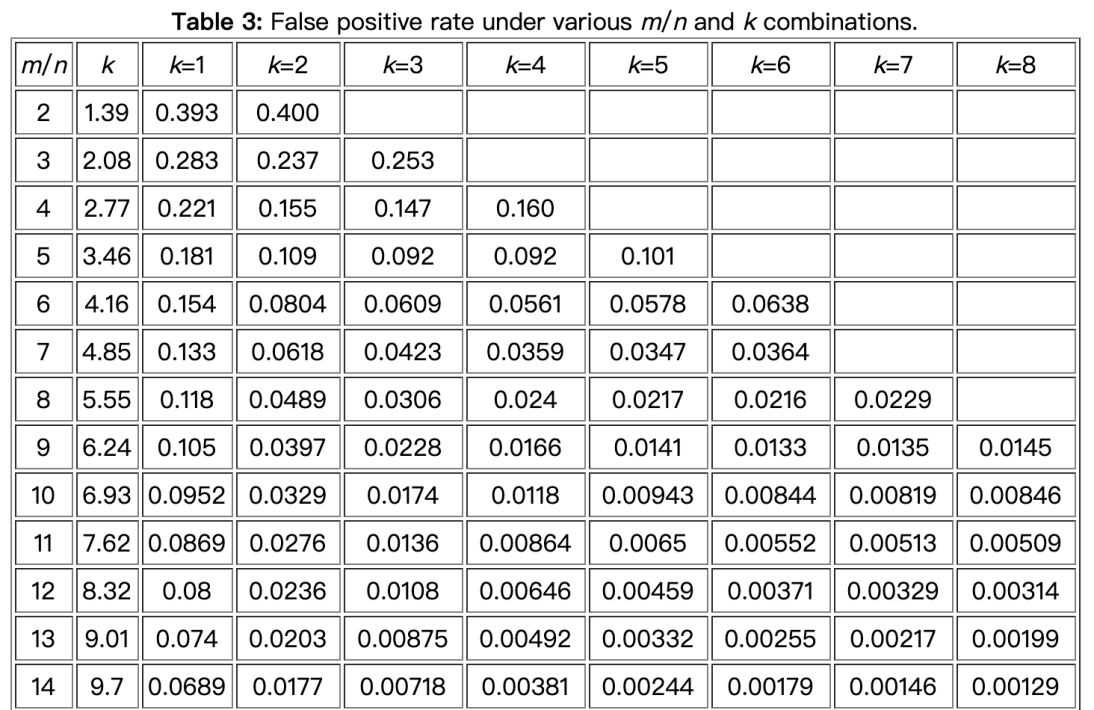
并且有如下结论:对于给定的m和n,k=m*ln2/n 时,假阳性的概率取值最小,也就是说并不见得哈希函数个数越多,假阳性概率就越低,而是有个最优解。
redis对bloomFilter的支持
redis没有直接提供BF等数据结构的支持,而是在Redis Modules中提供了支持。通过下载RedisBloom源码,编译后得到对应的so文件,然后在启动server加载这个so,就可以支持BF以及cuckoo filters和top-k等数据结构了。
安装RedisBloom
git clone https://github.com/RedisBloom/RedisBloom.git
cd RedisBloom
make
#编译之后得到redisbloom.so文件
#然后通过--loadmodule加载即可
./redis-server --loadmodule ../redisbloom.so然后可以通过:BF.ADD newFilter foo 以及BF.EXISTS newFilter foo命令来添加元素和判断元素是否在集合当中。
127.0.0.1:6379> BF.ADD test 1
(integer) 1
127.0.0.1:6379> BF.ADD test 2
(integer) 1
127.0.0.1:6379> BF.ADD test 3
(integer) 1
127.0.0.1:6379> BF.EXISTS test 1
(integer) 1
127.0.0.1:6379> BF.EXISTS test 4
(integer) 0
127.0.0.1:6379> BF.EXISTS test 5
(integer) 0
127.0.0.1:6379>此外,RedisBloom还提供一系列的客户端来支持不同的编程语言,比如我们可以通过python脚本来验证BF的假阳性概率是否在指定的范围内。可以先通过pip安装redisbloom客户端:pip install redis redisbloom,然后执行测试脚本。
# Using Bloom Filter
from redisbloom.client import Client
import uuid
TEST_KEY = 'bloom'
rb = Client()
# do clean
rb.delete(TEST_KEY)
# 指定假阳性概率和m数组的长度
rb.bfCreate(TEST_KEY, 0.05, 10000)
# do test
# 添加10000个整数
for i in range(1, 10000):
#uuid_str = str(uuid.uuid1()) + "-" + str(i)
rb.bfAdd(TEST_KEY, i)
error_count = 0
for i in range(10001, 20000):
if rb.bfExists(TEST_KEY, i):
# 如果存在肯定是出错了,即产生False Positive
print(str(i) + " exists...")
error_count = error_count + 1
else:
print(str(i) + " not exists...")
print("false positive[error count:" + str(error_count) + " error rate: " + str(format(float(error_count) / float(10000), '.2f')) + "]")输出结果:
...
19953 not exists...
19954 exists...
19955 not exists...
...
19998 not exists...
19999 not exists...
false positive[error count:256 error rate: 0.03]实际计算假阳性概率约为0.03。
总结
redis中的bitmap提供了一些直接操作字符串bit位的api,这类api能够很方便的在实际开发中解决很多问题。而redisbloom这个模块,使得redis真正支持布隆过滤器,以及支持删除的cuckoo filter。这类功能,在某些领域具有很大应用价值;在使用布隆过滤器的场景中,一定要考虑假阳性概率的情况,看看业务上是否能够容忍假阳性事件的出现。
参考
http://pages.cs.wisc.edu/~cao/papers/summary-cache/node8.html
http://sigmodrecord.org/publications/sigmodRecord/0603/p26-article-pey.pdf
本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!