redis中的三种不常见数据类型之hyperloglog
上次介绍了bitmap和bloomfilter,这次介绍一个在大数据领域比较常见的数据类型或者说一种算法——hyperLogLog。
HyperLogLog
介绍
redis中的HyperLogLog是一个基数计数器,在2.8.9及以上版本中提供。所谓基数(Distinct Value,简称DV)是指一个集合当中不相同元素的个数,而HyperLogLog就是这样一个计数器,能够用极小空间,来统计集合中不同元素的个数。和bitmap类似,在redis中,HyperLogLog也是一个字符串(为了标识这个字符串以HYLL打头)。
指令介绍
HyperLogLog的指令比较简单,只有三个:pfadd,pfcount以及pfmerge。
pfadd
用于向集合当中添加元素。
127.0.0.1:6379> pfadd test 1
(integer) 1
127.0.0.1:6379> pfadd test 1 2 3
(integer) 1
127.0.0.1:6379> pfadd test "hello world"
(integer) 1
127.0.0.1:6379> type test
string
127.0.0.1:6379> get test
"HYLL\x01\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x80]f\x80GN\x8cF$\x80Q,\x8cC\xf3"
127.0.0.1:6379>pfcount
用于统计集合的基数。
127.0.0.1:6379> pfcount test
(integer) 4
127.0.0.1:6379> pfadd test 4 5 6
(integer) 1
127.0.0.1:6379> pfcount test
(integer) 7
127.0.0.1:6379>pfmerge
用于合并多个hyperloglog,pfmerge deskey sourcekey1 sourcekey2...。
127.0.0.1:6379> pfadd test2 0.1 0.2
(integer) 1
127.0.0.1:6379> pfmerge test3 test test2
OK
127.0.0.1:6379> pfcount test3
(integer) 9
127.0.0.1:6379> pfcount test2
(integer) 2
127.0.0.1:6379> pfcount test
(integer) 7
127.0.0.1:6379>内存消耗
之前介绍过hyperloglog通过极小的内存就能计算非常大集合的基数。我们可以用之前计算DAU的场景来模拟一下,假如用hyperloglog来存储活跃用户的ID,看看占用多大空间。用如下脚本来创建5千万个字符串id,看看最终的value有多长。
#!/bin/bash
elements=""
key="test_hyperloglog"
for((i=1;i<=50000000;i++));
do
elements="${key}_uuid_"${i}
./redis-cli pfadd ${key} ${elements}
echo "add ${elements}"
done
echo "done."该脚本执行完比较耗时,(我这里没有执行完)在往redis中添加了14102763个字符串id后,最终的value字符串长度只有:12304,相当于12KB,可见hyperLogLog是很节省空间的。此外从pfcount得出的估计值:14261991,和实际值是有误差的,将近大了1.12%。
127.0.0.1:6379> strlen test_hyperloglog
(integer) 12304
127.0.0.1:6379> pfcount test_hyperloglog
(integer) 14261991
127.0.0.1:6379>算法原理
在介绍hyperloglog算法之前,可以先从生活中常见的一个例子讲起。如果有这样一个问题:假设某人抛了很多次硬币,并告诉我们在这次抛硬币的过程中最多只有两次扔出连续的反面,让我们猜总共抛了多少次硬币?

从感性上来看,如果只是连续两次反面,抛硬币的总次数应该不会很多,因为这种情况很容易出现;如果说是连续抛了10次都是反面,那么可以说明这个人很可能抛了特别多次,因为连续10次反面的情况并不多见。
如果要设计一个计算求抛硬币总数的算法,则可以通过如下思路进行设计:
定义一个二进制序列,假设1代表抛出正面,0代表反面。那么连续两次反面,则是连续出现两个0,由于是连续两个0,那么第三个应该就是1,那么必定出现的序列就是001,那么这样的概率就好计算了,就是(1/2)^3,也就是1/8,即这个人大概抛了8次硬币。
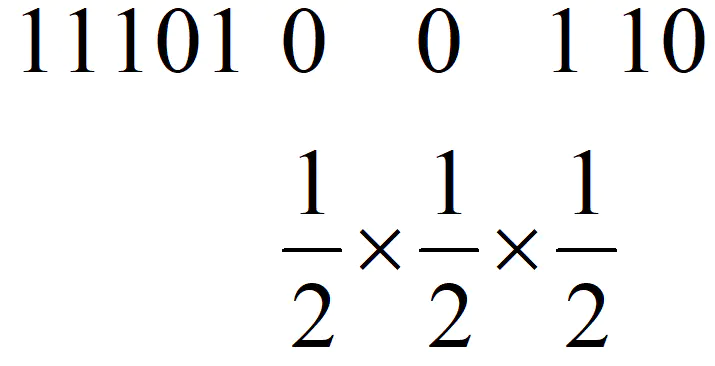
同样在计算机中,将某个对象的哈希值,转化为二进制,其中的0和1就和抛硬币比较类似了。不过为了简化,只取哈希值二进制中最前面连续的0的数量,即前导0。那么根据抛硬币受到的启发,求一个集合的基数,可以得到如下算法:
输入:一个集合
输出:集合的基数
算法:
max = 0
对于集合中的每个元素:
hashCode = hash(元素)
num = hashCode二进制表示中最前面连续的0的数量(前导0)
if num > max:
max = num
最后的结果是2的(max + 1)次幂上面这种做法虽然能够做一个大致的估算,但是显然误差是比较大的,很容易受到突发事件(比如突然连续抛出好多0)的影响,HyperLogLog之类的算法研究的就是如何减小这个误差。
分桶(LogLog)
最简单的一种优化方法显然就是把数据分成m个均等的部分,分别估计其总数求平均后再乘以m,称之为分桶。对应到前面抛硬币的例子,其实就是把硬币序列分成m个均等的部分,分别用之前提到的那个方法估计总数求平均后再乘以m,这样就能一定程度上避免单一突发事件造成的误差。
例如分桶个数为2,那么可以通过哈希值的第一位映射到不同的桶中,然后分别计算每个桶中前导0的最大值,然后计算前导0+1最大值的平均值得到最终解决。这种方法,在一定程度上可以减少偶然因素导致的误差影响。
hash(ele1) = 00110111
hash(ele2) = 10010001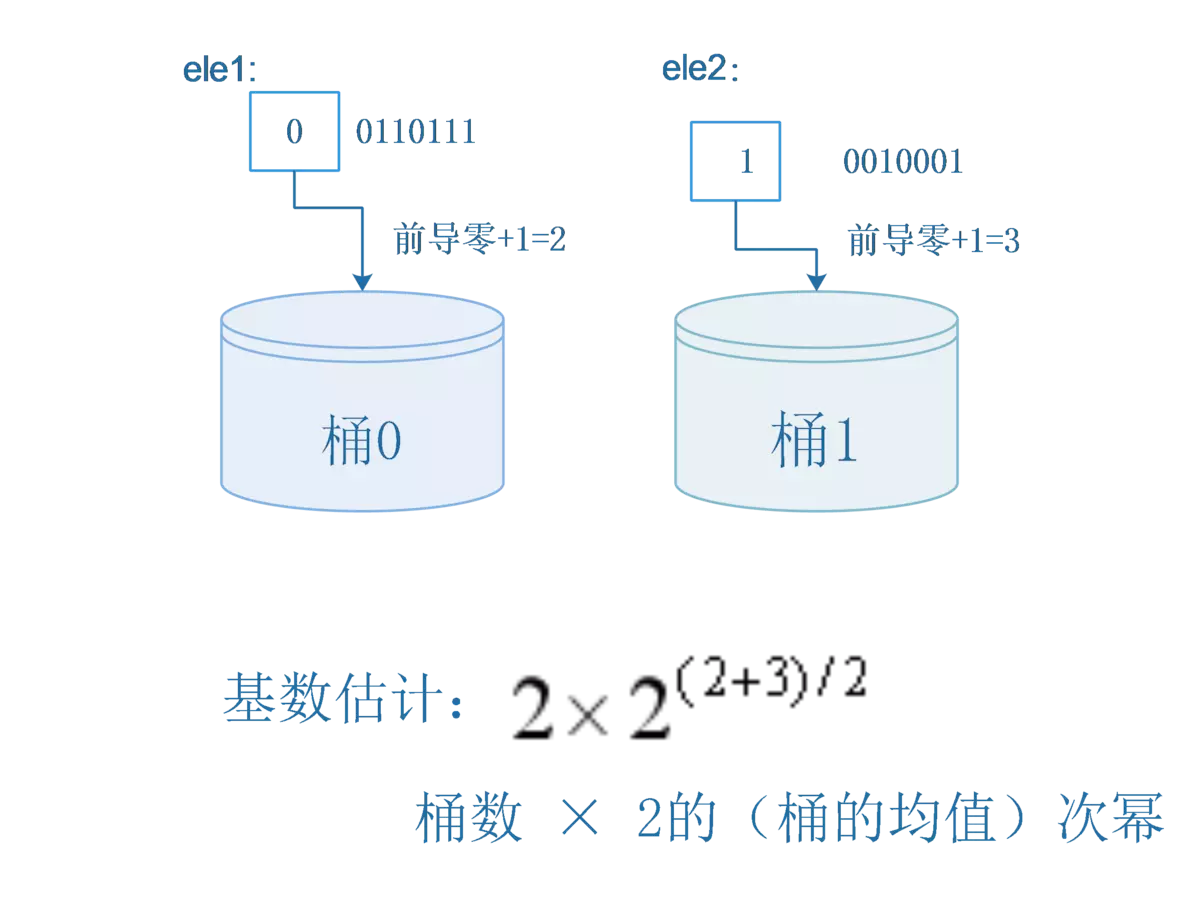
经过分桶的优化之后,该方法和LogLog算法很接近了,该算法的计算公式为:
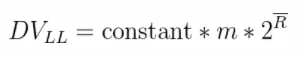
m:代表分桶数;
R:代表每个桶的结果(其实就是桶中数据的最长前导零+1)的均值
constant :修正常数修正常数的计算:先计算出:p = log2m。
switch (p) {
case 4:
constant = 0.673 * m * m;
case 5:
constant = 0.697 * m * m;
case 6:
constant = 0.709 * m * m;
default:
constant = (0.7213 / (1 + 1.079 / m)) * m * m;
}关于平均数
HyperLogLog算法对LogLog算法有一些改进,其中一个就是改进了平均数的计算方式。在LogLog算法中,每个分桶的前导0+1的平均方法采用的是最简单的算术平均法。
而对于平均数,不同的求法会导致计算结果不同。之前在知乎上看到一个关于平均数的讨论,挺有意思的:问题的场景是,某人每周需要买一次菜,有两种购买方式,一是每次买固定金额的,而是每次买固定重量的,问那种购买方式比较合算?
假设连续买菜n周,每周的菜价为ai
方式一,每周买菜重量固定为A,那么求平均价格:
A*(a1+ a2+…+an)/A*n=(a1+a2+…+an)/n
方式二,每周买菜金额固定为M,那么求平局价格:
nM/(M/a1+M/a2+…+M/an=n/(1/a1+1/a2+…+1/an)显然每次购买固定金额的,是比较合算的;一个比较感性的理解是,如果某天菜价上涨了,那么购买的就少;反之菜价便宜就购买的多,自然这种方式会合算些。实际上方式一求的是算术平均数,方式二,求的是调和平均数;除了这两种还有其他几种平均数的计算方式。它们的关系是:Hn <= Gn <= An <= Qn。
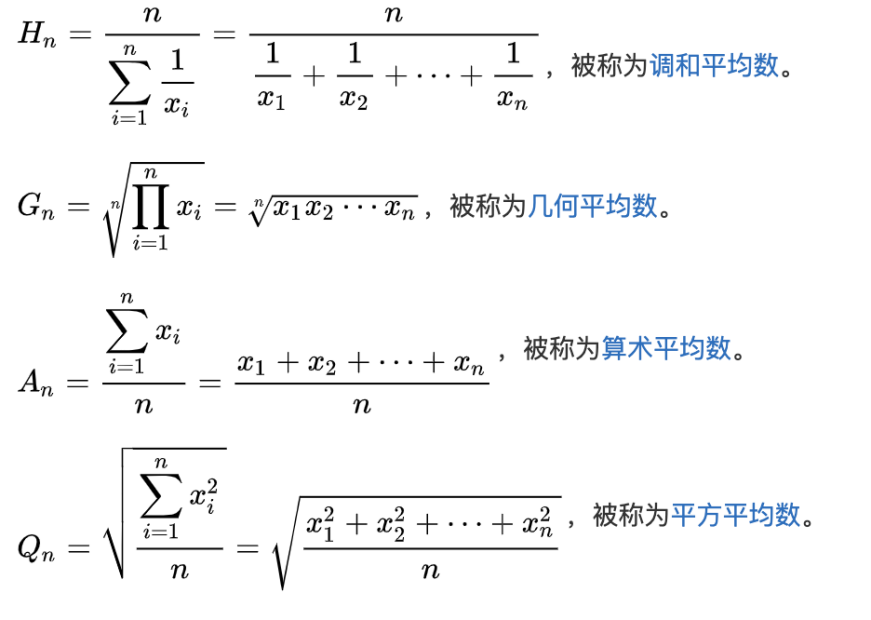
回到求集合基数的问题中,我们寻求一种比较好的平均数的计算方式,是为了减少偶然因素带来的误差,而这个误差会导致求的的结果偏大,显然可以用计算结果偏小的调和平均方式,来抵消一部分误差的影响。
采用调和平均数:
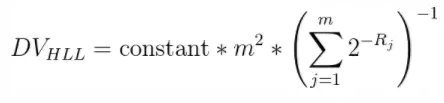
即:
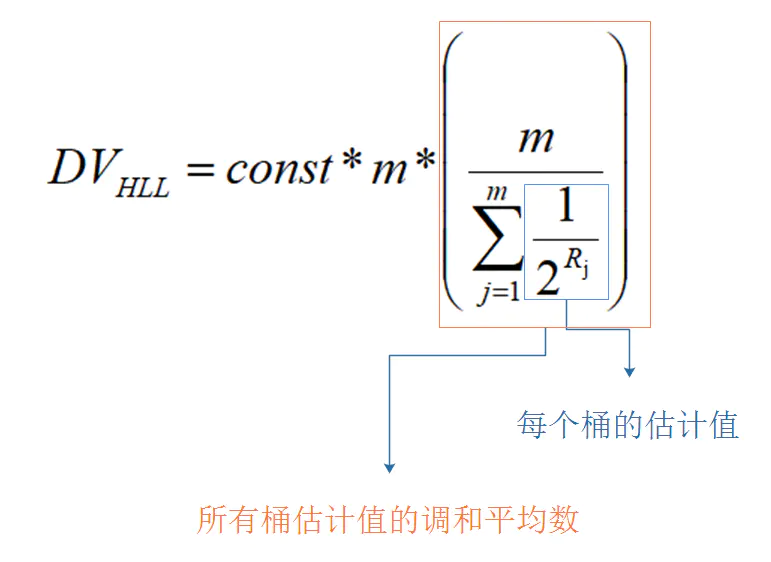
数据总量比较小的时候,很容易就预测偏大,hyperLogLog还有其他的微调。
if DVs < (5 / 2) * m:
DV = m * ln(m/V)DVs代表估计的基数值,m代表桶的数量,V代表结果为0的桶的数目,就是没有数据的桶。
网上有一个LL和HYLL算法的对比演示,做的很直观,可以参考下。
Redis官方给的错误率是:0.81%,我这里通过python脚本,实验了一下,误差率是比这个结果要大一些的。
测试脚本:
import redis
import uuid
TEST_KEY = 'hyperloglog'
TEST_FILE = "hyperloglog3.txt"
logfile = open(TEST_FILE, "w")
rediscli = redis.Redis(host='localhost', port=6379, decode_responses=True)
# clean
rediscli.delete(TEST_KEY)
print("before test count: " + str(rediscli.pfcount(TEST_KEY)))
# do test
for i in range(1, 1000001):
uuid_str = str(uuid.uuid1())
# print(str(i) + ": generate uuid: " + uuid_str)
rediscli.pfadd(TEST_KEY, uuid_str)
# logfile.write(str(i) + " : " + uuid_str + "\n")
if i % 10000 == 0:
logcount = rediscli.pfcount(TEST_KEY)
logfile.write("Actual Cardinality: " + str(i) + " Estimated Cardinality: " + str(logcount) + " Error%" + str(format(float((logcount - i) * 100) / float(i), '.2f')) + "\n")
logfile.close测试结果:
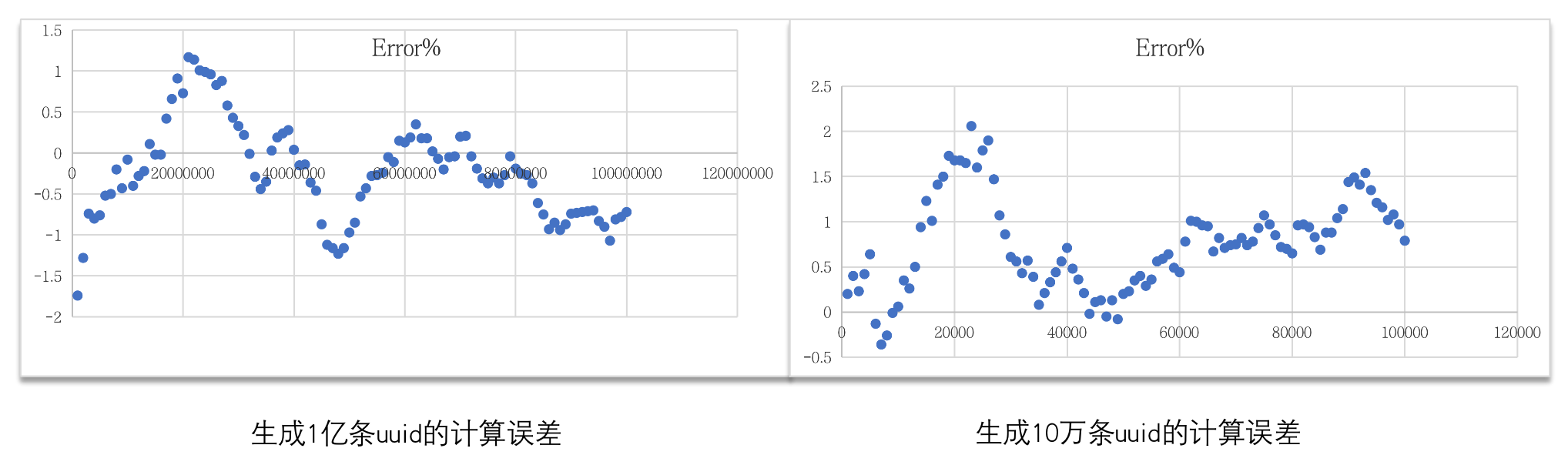
总结
hyperLogLog是一个利用概率统计来估算某个集合数据量的算法,有支持的数据量大,性能高,占用内存小的特点,由于是一个估算算法,所以没法得到精确值。
参考
本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!